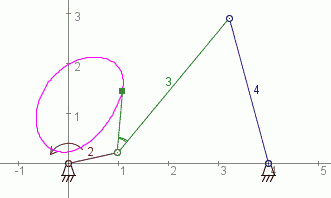
BWT Simulation
Ein Programm zur Getriebeanimation.
Das Programm baut auf den Paketen 'geometry' und
'mechanism' auf, welche im Rahmen eines Praktikums
im Nebenfach Bewegungstechnik an der TU-Dresden,
in Zusammenarbeit mit Thomas Ludwig entstanden sind.
Ein Programm zur Getriebeanimation.
Das Programm baut auf den Paketen 'geometry' und
'mechanism' auf, welche im Rahmen eines Praktikums
im Nebenfach Bewegungstechnik an der TU-Dresden,
in Zusammenarbeit mit Thomas Ludwig entstanden sind.
Download:
Das Programm als ausführbare *.jar Datei. [Version: 15.06.2007]
Das Applet als *.jar Datei. Applet-Demonstration und Infos
Was das Programm kann:
Was das Programm (noch) nicht kann:
Funktionen die mit Vorsicht zu genießen sind:
Weitere Tipps und Infos:
Das Programm als ausführbare *.jar Datei. [Version: 15.06.2007]
Das Applet als *.jar Datei. Applet-Demonstration und Infos
Was das Programm kann:
- Getriebeanimation für Koppelgetriebe mit Dreh- und Schubgelenken
- Zeichnen von Koppelkurven
- Bestimmung von Momentanpolen, Wendekreis, Wendepol, BALLschen Punkt und
Ersatzgetrieben (nach Satz von ROBERTS) für ein viergliedriges Getriebe - Laden und Speichern von Getrieben im XML Format
- Einbindung in eine Webseite mit Anzeige eines Hintergrundbildes (Applet-Version)
Was das Programm (noch) nicht kann:
- Unterstützung von Schubantrieben (Implementierung fehlt noch)
- Getriebeanalyse (Geschwindigkeiten, Beschleunigungen, Kräfte)
Funktionen die mit Vorsicht zu genießen sind:
- Berechnung von Getrieben, welche nicht vollständig aus Zweischlägen
zusammengesetzt sind. (Siehe: 'Test: 6 Gelenk (Antrieb 61, ...)'
Diese Funktion ist noch sehr experimentell!) - Zuordnung der Antriebe bei Ersatzgetrieben nach ROBERTS.
(In Spezialfällen ist der Antrieb evtl. an der falschen Stelle.)
Weitere Tipps und Infos:
- Programmbedienung:
Wenn die linke Maustaste gedrückt wird, kann mit Mausbewegung das Koordinatensystem verschoben werden. Wird die rechte Maustaste gedrückt, kann mit Mausbewegung das Koordinatensystem gezoomt werden (alternativ auch mit dem Scrollrad).
Es gibt außerdem zahlreiche Tastenkombinationen ([Strg + M] zeigt z.B. Momentanpole an) - Getriebeaufbau:
Ein Getriebe besteht im Programm aus einer Menge von Gliedern, wobei das zuerst definierte Glied das Gestell darstellt. Jedes dieser Glieder hat eine bestimmte Menge von Gelenk-Objekten die untereinander verknüpft werden. Die Positionen der Gelenk-Objekte sind relativ zum Koordinatensystem des Gliedes definiert.
Ein Viergelenk hat somit im Programm 8 Gelenk-Objekte. Jede Verbindung XY besteht aus einem Gelenk im Glied X und einem Gelenk im Glied Y. - Drehantriebe (Welches Gelenk-Objekt ist der Antrieb?):
Ein Antrieb ist das Gelenk-Objekt des Gliedes welches angetrieben wird. Bei einem Antrieb im Punkt A0 ist also das Gelenk-Objekt im Glied 2 welches mit Glied 1 verbunden ist der Antrieb. - Drehantriebe (Wo wird der Antriebswinkel angetragen?):
Befindet sich der Drehantrieb im Koordinatenursprung des Getriebegliedes, so wird die X-Achse des Glied-Koordinatensystems angetrieben. Sollte sich der Punkt nicht an der Stelle (0,0) befinden, so wird die Gerade zum Koordinatenursprung angetrieben. Das Einblenden der 'Antriebsgrundlinien' zeigt die Linien an, zwischen denen der Antriebswinkel angetragen wird. - Beispiel (Definition einer Kurbelschwinge im XML Format.): Komplette XML Datei mit DTD
<Getriebe_Export>
<Getriebe name="Kurbelschwinge">
<Getriebeglied>
<Drehgelenk id="12" verbundenMitGelenkID="21" />
<Drehgelenk id="14" verbundenMitGelenkID="41" xKoordinate="4.0" />
</Getriebeglied>
<Getriebeglied>
<Drehantrieb id="21" verbundenMitGelenkID="12" />
<Drehgelenk id="23" verbundenMitGelenkID="32" xKoordinate="1.0" />
</Getriebeglied>
<Getriebeglied>
<Drehgelenk id="32" verbundenMitGelenkID="23" />
<Drehgelenk id="34" verbundenMitGelenkID="43" xKoordinate="3.5" />
<Koppelpunkt xKoordinate="1.0" yKoordinate="0.7" />
</Getriebeglied>
<Getriebeglied>
<Drehgelenk id="43" verbundenMitGelenkID="34" />
<Drehgelenk id="41" verbundenMitGelenkID="14" xKoordinate="3.0" />
</Getriebeglied>
</Getriebe>
</Getriebe_Export>
- Fehler im Programm:
Es kann nicht garantiert werden, dass das Programm korrekte Ergebnisse liefert.
Sollte es noch Fehler im Programm geben, wäre ich über eine Info dankbar.
Home :: BWT Simulation
nach oben